Abstract
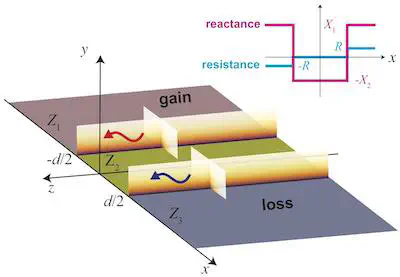
Line waves are recently discovered wave entities that are localized along two directions and therefore can be viewed as the one-dimensional counterpart of surface waves. These waves can be supported at discontinuities of the surface reactance and/or resistance of low-dimensional materials such as metasurfaces or graphene. Here, a broader class of non-Hermitian surface-impedance junctions is studied that can support coupled line waves and that allows the investigation of different one-dimensional waveguiding mechanisms in a unified framework. It is theoretically demonstrated that, under parity–time-symmetry conditions, exceptional points can occur in a truly flat-optics scenario, hence endowing these waveguiding systems with the attractive features of both line-wave and exceptional-point physics and shedding further light on the phase transitions existing in these systems. It is also shown that the required surface-impedance parameters are compatible with those attainable with typical models of photoexcited graphene metasurfaces at terahertz frequencies. Besides providing additional understanding in the physics of line waves, which is still in its infancy, these results pave the way toward intriguing developments in the largely unexplored field of non-Hermitian flat optics, with possible applications ranging from sensing to lasing and on-chip optical signal processing.