Abstract
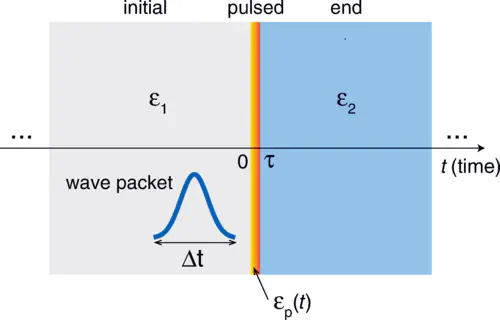
We study a class of temporal metamaterials characterized by time-varying dielectric permittivity waveforms of duration much smaller than the characteristic wave-dynamical timescale. In the analogy between spatial and temporal metamaterials, such a short-pulsed regime can be viewed as the temporal counterpart of metasurfaces. We introduce a general and compact analytical formalism for modeling the interaction of a short-pulsed metamaterial with an electromagnetic wave packet. Specifically, we elucidate the role of local and nonlocal effects, as well as the time-reversal symmetry breaking, and we show how they can be harnessed to perform elementary analog computing, such as first and second derivatives. Our theory validated against full-wave numerical simulations suggests a novel route for manipulating electromagnetic waves without relying on long, periodic temporal modulations. Just as metasurfaces have played a pivotal role in the technological viability and practical applicability of conventional (spatial) metamaterials, short-pulsed metamaterials may catalyze the development of temporal and space-time metamaterials.